Binary Indexed Tree, BIT ( Single Point Modification, Interval Summation )

Why to use

• More quick, more fast

• Apply to interval summation, so if you use array ( $O (n^2)$ ) or prefix-summation ( modification $O(n)$ , query of interval summation $O(1)$ ), so when the $n$ is very big, it will be slow.

Binary Indexed Tree

Operations

1. $add ( i , k )$ $\space\space\space\space$ ( $1\le i\le n$ ) $\space\space\space\space$ add $k$ to the values of $i$ elements

2. $sum (i)$ $\space\space\space\space$ ( $1\le i\le n$ ) $\space\space\space\space$ calculate the sum of range $(1,i)$

Basic Properties

1. Firstly, BIT is a kind of array, also a kind of tree.

2. Secondly, BIT stored in memory as an array.

3. Thirdly, for two array index $x\space ,\space y$, if $x + 2^k = y$ ( k is the number of 0 of $(x)_2$ ), so we define $(y,x)$ is a couple father and son on tree. In this, y is the father, x is the son.

Store

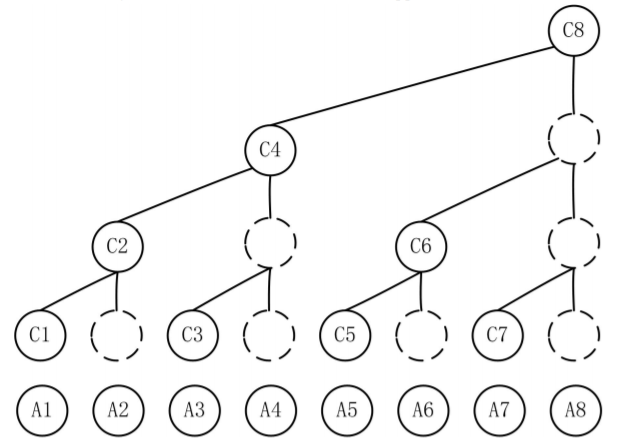
Like this. $c_i$ shows son-tree's leaves summation.

So:

$c_1$ = $a_1$

$c_2$ = $a_1$ + $a_2$

$c_3$ = $a_3$

$c_4$ = $a_1$ + $a_2$ + $a_3$ + $a_4$

$c_5$ = $a_5$

$c_6$ = $a_5$ + $a_6$

$c_7$ = $a_7$

$c_8$ = $a_1$ + $a_2$ + $a_3$ +$a_4$ + $a_5$ + $a_6$ + $a_7$ + $a_8$

If we change the array-$c$ to binary:

(1 = 001)

(2 = 010)

(3 = 011)

(4 = 100)

(5 = 101)

(6 = 110)

(7 = 111)

(8 = 1000)

We could find out that: $c_i = a_{i-2^k+1} + a_{i-2^k+2} +...+a_i$ ($k$ is the binary of $i$ the successive $0$ from low-digit to high-digit)

BIT Query Intercal Summation

$sum_7 = c_4 + c_6 + c_7$

eqauls

$sum_{(111)_2} = c_{(111)_2} + c_{(110)_2} + c_{(100)_2}$

• So, we could add some elements of array $c$ to get the intercal summation.

• lowbit (i)

  Get the value of $2^k$. $k$ is the binary of $i$ the successive $0$ from low-digit to high-digit.

• While the $n$ is more bigger, BIT's goodness is more clearly.

• We can "minus" the $0$ at the end of the binary of $i$, that means we need to minus $2^k$.

inline int sum ( int x ) {
    int ans = 0 ;
    while ( x > 0 ) {
        ans += c[x] ;
        x -= lowbit (x) ;
    }
    return ans ;
}

BIT Single Point Modification

• While we change array $a$, we need to update array $c$. It will be a reverse process of sum(i).

inline void add ( int x , int d ) {
    while ( x <= n ) {
        c[x] += d ;
        x += lowbit (x) ;
    }
}

Time Complexity

Modification & Summation

• In add ( x , d ), we need add $d$ to each $c_i$ interval containing $a_x$. As same as in sum (x), we need to count the sum of $O(\log n)$ intervals.

• In lowbit (x), every time you deal with an interval, you need a lowbit (x) function. So it's $O(\log n)$ too.

Lowbit Function

• Simple version of lowbit (x) function:

inline int lowbit ( int x ) {
    int ans = 1 ;
    while ( x % 2 == 0 ) {
        x /= 2 ;
        ans *= 2 ;
    }
    return ans ;
}

Summary

So, if you use the simple version of lowbit (x) function, the sum time complexity will be $O(\log^2 (n))$

More Quick Of Lowbit

• We can use complement code to calculate it.

• Code:

inline int lowbit ( int x ) {
    return x & -x ;
}

• So now the time complexity is $O(\log n)$, memory complexity $O(n)$.

BIT Extention

Interval Modification, Single Point Query

1. $add ( x , y , k )$ $\space\space\space\space$ ( $a_i += k$ , $x\le i\le y$ ) $\space\space\space\space$ add $k$ to the elements in interval $[x,y]$.

2. $get (x)$ $\space\space\space\space$ ( print $a_x$ ) $\space\space\space\space$ query the value of element $x$.

Single Point Modification & Interval Modification

• We can use difference to solve this problem, turn what array element $sum_n$ wants to the value of $a_n$. Solution like the down text.

• We use array $b$ to:

  • If $n$ eqauls $1$, $b_1 = a_1$

  • If $n > 1$, $b_n = a_n - a_{n-1}$

  • We get array $sum$ use BIT on array $b$, then $sum_n = a_n$

Single Point Query & Interval Summation

• Like last page, it also can use difference to solve the problem.

• We don't need every elements add on a $k$. You see, $a_i = b_1 + b_2 + ... + b_i$, when we add $k$ on left, we just need to add only one k on right to keep it's balance.

• So, if we want to add k on the elements of $a_x$ to $a_y$, we should: $b_x += k; b_{y + 1} -= k;$.