Segment Tree

Why to use

• It can handle more kind of query and modification, but, it is not faster than BIT ( Binary Indexed Tree ).

• Although the code is longer than BIT ( BIT: 50+ ~ 60- lines ; Segment Tree: 130+ lines ), but the code structure is very clear. That means, if you realy know what it works, you can type the code easily.

Diffrence of them

• For exanple, Single Point Modification, Interval Summation.

• Use BIT to solve this problem:

CodeLenth Time Memory
1.03KB 543ms 4.36MB

• Use Segment Tree to solve this problem:

CodeLenth Time Memory
2.91KB 377ms 9.61MB

• It seems that Segment Tree is just faster than BIT a little bit, except that, Segment Tree need the double memory of BIT, and nearly triple code lines.

• You may think Segment Tree is useless; but if you realy know it, you'll love it forever.

Segment Tree

Structure

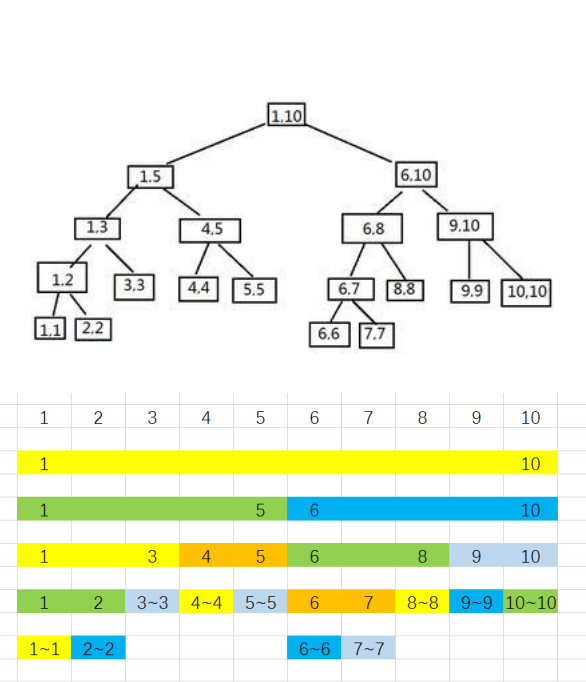
• The most fundamental thought of Segment Tree is, sort the big interval into small interval, then modify & query on these small interval.

Build Tree

• The process of sorting can build a tree. So now we think: every point on this tree have got what information ?

• First, the leftbound and rightbound of the interval that it was sorted. Second, the sum of the interval ( interval summation ). Third, the leftchild and rightchild of this point. Of course, if this point is a leave, it nether got a leftchild nor rightchild.

• In the code, we use array leftn to store leftbound of the point, use array rightn to store rightbound of the point. Use sum to store interval summation, and k << 1 means leftchild's array index, k << 1 | 1 means rightchild's array index.

• The time complexity of the part is $O (\log n )$, also, the high of tree is $\log n$ too.

$Code$

inline void build ( int k , int leftbound , int rightbound ) {
    leftn[k] = leftbound , rightn[k] = rightbound ;
    if ( leftbound == rightbound ){
        sum[k] = a[leftn[k]] ;
        return ;
    }

    int mid = ( leftn[k] + rightn[k] ) >> 1 ;
    build ( k << 1 , leftn[k] , mid ) ;
    build ( k << 1 | 1 , mid + 1 , rightn[k] ) ;

    sum[k] = sum[k << 1] + sum[k << 1 | 1] ;
}

Interval Summation, Single point Modification

Single point Modification

• Every time we modify a single point, we go down from the root point, find the element ( it's a point on the tree ) that we need to modify and modify it. When it was modified, we go up from this point and update every father point's interval summation.

• Because of the tree-height is $\log n$, and every time we modify need go down once and go up once, so the time complexity of this part is $O (\log n )$.

$Code$

inline void update ( int k , int leftbound , int rightbound , long long x ) {
    if ( leftbound <= leftn[k] && rightn[k] <= rightbound ) {
        sum[k] += x ;
        return ;
    }

    int mid = ( leftn[k] + rightn[k] ) >> 1 ;
    if ( leftbound <= mid ) {
        update ( k << 1 , leftbound , rightbound , x ) ;
    }
    if ( mid + 1 <= rightbound ) {
        update ( k << 1 | 1 , leftbound , rightbound , x ) ;
    }

    sum[k] = sum[k << 1] + sum[k << 1 | 1] ;
}

Interval Summation

• Like the part before, we need go down to find the element which in the interval that we query, and collect answer when go down.

$Code$

inline long long query ( int k , int leftbound , int rightbound ) {
    if ( leftbound <= leftn[k] && rightn[k] <= rightbound ) {
        return sum[k] ;
    }

    long long ans = 0 ;
    int mid = ( leftn[k] + rightn[k] ) >> 1 ;

    if ( leftbound <= mid ) {
        ans += query ( k << 1 , leftbound , rightbound ) ;
    }
    if ( mid + 1 <= rightbound ) {
        ans += query ( k << 1 | 1 , leftbound , rightbound ) ;
    }

    return ans ;
}

Complete Segment Tree To Binary Tree

• Why need do this? No thing to do?

  • While we use array to store a tree, we need to conect the elements in tree. So, if we don't leave a place for the empty point, the structure of array will be ambiguity.

• When we complete Segment Tree to Binary tree, we will need fourfold memory.

• Why? Just think that $k$ is the value of $\lfloor \log n \rfloor$, so $2^k < n < 2^{k+1}$, when the high of Segment Tree is $k + 1$, we can't put all element of array in the leaf-point. That means, the tree-height must be $k + 2$, at the moment, the number of nodes will be $2^{k + 2}$.

• If you calculated the number of nodes, you'll find out that it's almost the fourfold of the number of elements.

The Tag Of Segment Tree ( Apply To Interval modification )

• Problem: interval modification, interval summation

Use Thing That We Have Learned

• Interval modification: point-by-point modify on tree.

• Interval summation: just query on tree.

• Time complexity: $\mathcal{O} ( n^2 \times \log n )$

• $\mathfrak{}{IT\space IS\space EVEN\space WORSE\space THAN\space SILLY\space ENUMERATION\space !\space !\space ! }$

Lazy Tag

To be a "tag", why you are lazy? Because this part is the most important part of Segment Tree, so this part I'll explain it as detailed as I can.

Preface

• Interval modification, this operation has got a characteristic - that is, this operation use the same rule to modify the elements in this interval. So we just need tell a point on the tree: we need to do the same operation to modify the elements in your interval. And then, we mark this opearation, we do it when we need it.

More Simple Description

• For exanple, if you want to do add 3 and add 5 these two operation. If don't use lazy tag, we need to update the sub-tree twice - that means, to every operation, we need do it when we get the instruction.

• So, if we update the segment tree like the programme before, we're wasted a lot of time, the time complexity is very high. The function of lazy tag is, when we get the instruction add 3, we just put it in the tag, when we need to get the sum of the interval, we do the calculation.

• And, if we get another instruction, we just add it into the [interval that we need to update]'s lazy tag.

Nearly The Code

• The translate of lazytag just like the DP equation. To the different problem, we need different translate equation.

• Simplely, we have some fixed translate equation. You can see it like a rule.